
The column space of A is the subspace of R m spanned by the columns of A.So every subspace is a vector space in its own right, but it is also defined. Īny matrix naturally gives rise to two subspaces. A subspace is a vector space that is contained within another vector space. Therefore, all of Span a spanning set for V. If u, v are vectors in V and c, d are scalars, then cu, dv are also in V by the third property, so cu + dv is in V by the second property.


There are a number of other cases that can be treated ad-hoc, if one is a hyperplane, or the dihedral angle between planes in R 3. 1) non-empty (or equivalently, containing the zero vector) 2) closure under addition. The 'rules' you know to be a subspace Im guessing are.
SUBSPACE DEFINITION PLUS
This has a fairly obvious meaning if E 1 is 1-diemsnional: Take the angle between any non-zero vector in E 1 and its orthogonal projection onto E 2. A nonempty subset W of V is said to be a subspace of V if, using the plus and scalar multiplication. The definition of a subspace is a subset that itself is a vector space. In other words the line through any nonzero vector in V is also contained in V. 1) non-empty (or equivalently, containing the zero vector) 2) closure under addition 3) closure under scalar multiplication.3 answers Top answer: The definition of a subspace is a subset that itself is a vector space. I want to define the angle between two subspaces E 1 and E 2. If v is a vector in V, then all scalar multiples of v are in V by the third property.Īs a consequence of these properties, we see: 4.The subspace topology on (0 1) R induced by the usual topology on R is the topology generated by the basis B (0 1) f(a b) : 0 a 
Since each Wi is a subspace, we then learn that for all a, b F.
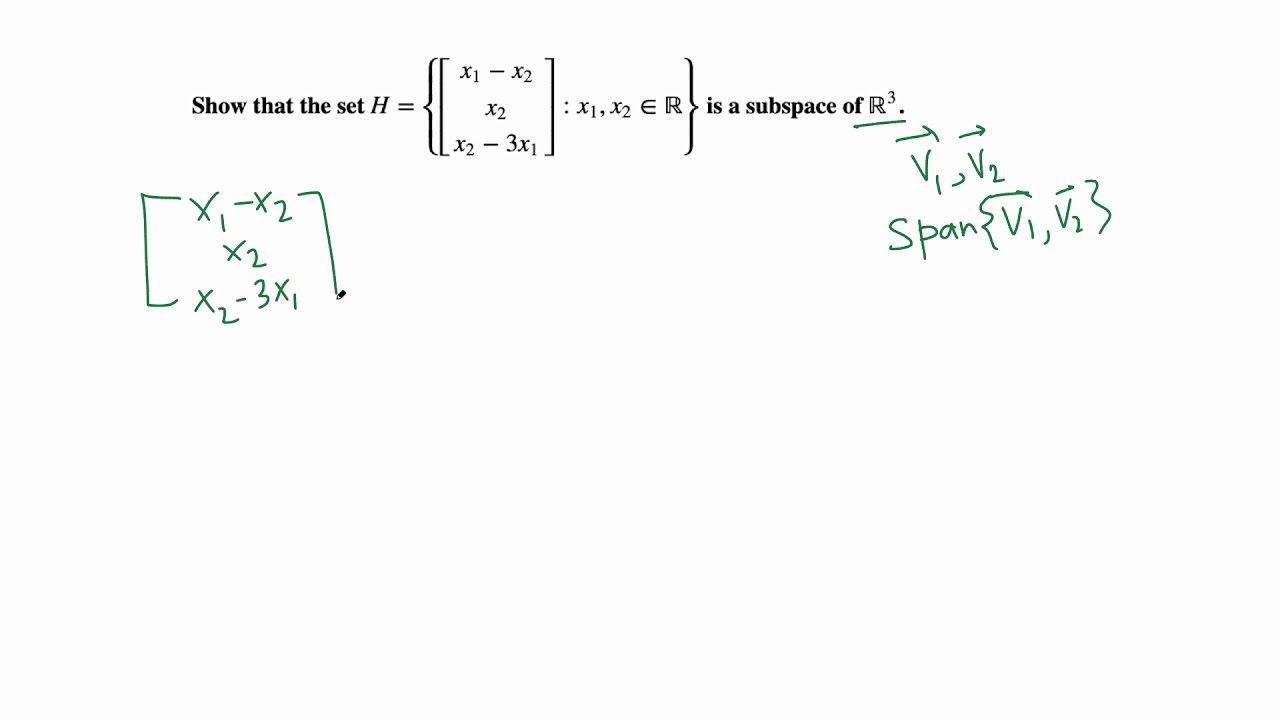
We say that U is a subspace of V if U is closed under. If W is a subset of a vector space V and if W is itself a vector space under the inherited operations of addition and scalar multiplication from V, then W is called a subspace. Let V be a vector space over a field F and let U be a subset of the elements of V.


 0 kommentar(er)
0 kommentar(er)
